之前第4章介绍了矩阵的大部分重要属性和操作,并讨论了如何使用矩阵来表示一般的几何变换。第5章详细讨论了矩阵和几何变换。本章将通过讨论一些更有趣和有用的矩阵运算来结束矩阵主题。
- 第6.1节将介绍矩阵的行列式。
- 第6.2节将解释矩阵的逆矩阵。
- 第6.3节将讨论正交矩阵。
- 第6.4节将介绍齐次矢量和4×4矩阵,并演示如何将它们应用于三维中执行仿射变换。
- 第6.5节将讨论透视投影,并展示如何使用4x4矩阵进行透视投影。
6.1 矩阵行列式
对于方形矩阵,有一个特殊的标量称为矩阵的行列式(Determinant)。行列式在线性代数中有许多有用的属性,在几何中也有一些有趣的解释。
按照习惯,我们将首先讨论一些数学,然后做一些几何解释;第6.1.1节将介绍行列式的符号,并给出用于计算2×2或3×3矩阵的行列式的线性代数规则;第6.1.2节将讨论子矩阵行列式(Minor)和余子式(Cofactor);第6.1.3节节将展示如何使用子矩阵和余子式计算任意nxn矩阵的行列式;第6.1.4节将从几何角度解释行列式。
6.1.1 关于2×2和3×3的行列式
- 方形矩阵
的行列式表示为 ,有些图书也将它表示为"det "。非方形矩阵的行列式是未定义的。本节将介绍如何计算2×2和3×3矩阵的行列式。第6.1.3节将讨论相当复杂的一般性 矩阵的行列式。
的行列式由下式给出:

(当编写矩阵的行列式时,将使用垂直线代替括号)- 使用下面的示意图可以更容易地记住式(6.1)。只需沿对角线和反对角线分别让元素相乘,然后使用对角线元素相乘的结果减去反对角线元无素相乘的结果即可。

- 使用下面的示意图可以更容易地记住式(6.1)。只需沿对角线和反对角线分别让元素相乘,然后使用对角线元素相乘的结果减去反对角线元无素相乘的结果即可。
的行列式由下式给出:

- 我们可以通过一个类似的示意图来帮助记忆式(6.2)。先并排编写矩阵
的两个副本,然后沿对角线和反对角线分别让元素相乘,最后使用对角线元素相乘的结果的和减去反对角线元素相乘的结果即可。
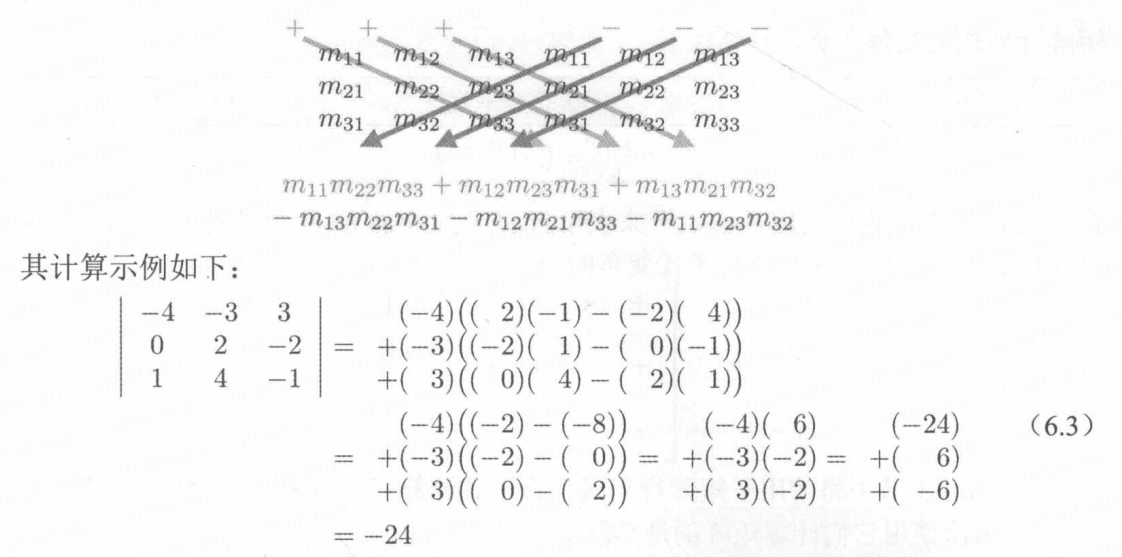
- 我们可以通过一个类似的示意图来帮助记忆式(6.2)。先并排编写矩阵
- 如果将
矩阵的行解释为3个矢量,那么该矩阵的行列式就等价于3个矢量的所谓三重积(TripleProduct),具体如下:
