3D数学基础-图形和游戏开发-学习笔记 第四章 矩阵简介

矩阵在3D数学中具有根本意义上的重要性,它们主要用于描述两个坐标空间之间的关系。它们通过定义将矢量从一个坐标空间转换为另一个坐标空间来实现此目的。

本章主要介绍矩阵的理论和应用。当引入矢量时，我们的讨论将遵循第2章中设置的模式:先介绍数学定义，然后提供几何解释。本章主要分为以下3节:

• 第4.1节将严格从数学角度讨论矩阵的一些基本属性和操作(更多矩阵运算将在第6章中讨论)。
• 第4.2节将解释如何以几何方式解读这些属性和操作。
• 第4.3节将本书中矩阵的使用放在更大的线性代数领域中来考查。

4.1 矩阵的数学定义

在线性代数中，矩阵是排列成行和列的矩形数字网格。前文将矢量定义为数字的一维数组，矩阵同样可以定义为数字的二维数组(Two-Dimension Aray)。“二维数组”中的“二”来自于行和列，不应与二维矢量或矩阵混淆。因此，矢量是标量的数组，而矩阵则是矢量的数组。
下面将分8个小节介绍矩阵，

• 第 4.1.1节将介绍矩阵维度的概念，并描述一些矩阵表示法。
• 第 4.1.2节将描述方形矩阵。
• 第 4.1.3 节将矢量解释为矩阵。
• 第 4.1.4节将描述矩阵转置。
• 第 4.1.5 节将解释如何将矩阵乘以标量。
• 第 4.1.6节将解释如何将矩阵乘以另一个矩阵。
• 第 4.1.7节将解释如何将矢量乘以矩阵。
• 第 4.1.8 节将比较行和列矢量的矩阵。

4.1.1 矩阵维度和表示法

1. 对于具有$r$行和$c$列的矩阵,称为是$r \times c$(读作“$r$乘$c$”)，例如下面的4×3矩阵。
   
2. 用大写字母表示矩阵变量，如$\pmb{M}、\pmb{A}、\pmb{R}$，而矩阵中的元素则使用下标表示法，通常使用小写斜体字母。
   

4.1.2 方形矩阵

1. 具有相同行数和列数的矩阵称为方形矩阵。
2. 方阵的对角元素是行和列索引相同的元素，例如3×3矩阵$\pmb{M}$的对角元素是$m_{11},m_{22},m_{33}$，其他元素是非对角元素
   
3. 如果矩阵中的所有非对角元素都为零，则该矩阵为对角矩阵(DiagonalMatrix)。以下4x4矩阵就是一个对角矩阵:
   
4. 对角线上的值为1，其他元素均为0，且为$n\times n$矩阵，则称为单位矩阵，表示为$\pmb{I}_{n}$，一般上下文清楚的情况下可以省去下标$n$，即$\pmb{I}$
   
5. 单位矩阵在矩阵中的意义就相当于标量中的1，任何矩阵乘以单位矩阵都等于自身。

4.1.3 作为矩阵的矢量

1. 矩阵可以包含任何正数的行和列，这个正数也可以是1。
2. 一行或一列的矩阵也可被称为矢量，维数n的矢量可以被是为1×n矩阵，或者n×1的矩阵。1×n矩阵称为行矢量，n×1称为列矢量。
   

4.1.4 矩阵转置

1. 给定$r\times c$矩阵，$\pmb{M}$的转置(Transpose)表示为$\pmb{M}^{T}$，是$c\times r$矩阵，其中，列由$\pmb{M}$的行构成。换句话说，$\pmb{M}=\pmb{M}^{T}$。这实际上是以对角方式“翻转”矩阵。以下式(4.1)和式(4.2)显示了两个转置矩阵的例子:
   
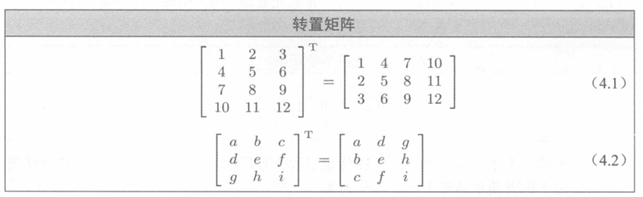
2. 对于矢量，转置会将行矢量转换为列矢量，反之亦然。列矢量一般会用转置表示法写成$[a,b,c]^T$
   
3. 转置的特性：
   • 对于任何维度的矩阵$\pmb{M}$,则$(\pmb{M}^{T})^{T}=\pmb{M}$。即如果先转置矩阵，然后再转置一次，即可得到原始矩阵。
   • 任何对角矩阵$\pmb{D}$等于其转置：$\pmb{D}_{T}=\pmb{D}$。单位矩阵$\pmb{I}$也是。

4.1.5 矩阵与标量相乘

矩阵$\pmb{M}$可以与标量$k$相乘，得到与$\pmb{M}$相同维度的矩阵。结果矩阵 $k\pmb{M}$中的每个元素是$k$与$\pmb{M}$中相应元素的乘积。例如，

4.1.6 两个矩阵相乘

1. 两个矩阵$\pmb{A}、\pmb{B}$相乘时，需要满足$\pmb{A}$的列数与$\pmb{B}$中的行数相等，否则无法相乘。
2. 矩阵乘法的计算如下：
   设矩阵$\pmb{C}$为$r\times n$矩阵$\pmb{A}$与$n\times c$矩阵$\pmb{B}$的$r\times c$乘积$\pmb{AB}$。然后每个元素$c$等于$\pmb{A}$的行$i$与$\pmb{B}$的列$j$的矢量点积，其用计算公式表述如下:
   $c_{ij}=\sum\limits_{k=1}^{n}a_{ik}b_{kj}$
   简单的描述一下:对于结果中的每个元素$c$，找到$\pmb{A}$中的第$i$行和$\pmb{B}$中的第$j$列:将行和列的相应元素相乘，并对积求和,$c$等于此总和，它相当于
   $\pmb{A}$中第$i$行和$\pmb{B}$中的第$j$列的点积。例如
   
   
   
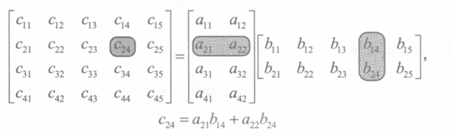
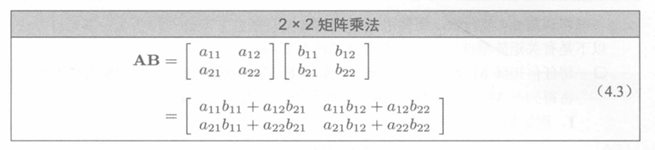
3. 矩阵乘法的总结：
   • （1）将任何矩阵$\pmb{M}$乘以一个方形矩阵$\pmb{S}$($\pmb{S}$放在哪一边都可以，即$\pmb{MS}$或$\pmb{SM}$都行)将得到与$\pmb{M}$ 大小相同的矩阵，条件是矩阵的大小允许乘法。如果$\pmb{S}$是单位矩阵$\pmb{I}$，则结果是原始矩阵$\pmb{M}$:
     $\pmb{M}\pmb{I}=\pmb{I}\pmb{M}=\pmb{M}$
   • （2）矩阵乘法不可交换（没有交换律）
     $\pmb{A} \pmb{B} \neq \pmb{B} \pmb{A}$
   • （3）矩阵乘法可以结合（有结合律），可以拓展到多个矩阵相乘的情况
     $\pmb{(AB)} \pmb{C} = \pmb{A} \pmb{(BC)}$
   • （4）矩阵乘法可以与标量或矢量结合
     $(k\pmb{A}) \pmb{B}=k(\pmb{AB})=\pmb{A} (k\pmb{B})，\pmb{(vA)} \pmb{B}=v\pmb{(AB)}$
   • （5）转置两个矩阵的乘积与以相反顺序取得其转置的乘积相同，可以拓展到多个矩阵转置的情况
     $\pmb{(AB)}^T=\pmb{B}^T\pmb{A}^T$

4.1.7 矢量和矩阵相乘

1. 由于矢量可以被认为是具有一行或一列的矩阵，因此可以通过第4.1.6节中讨论
   的规则将矢量和矩阵相乘。
   
   不难发现，当将左侧的行矢量乘以右侧的矩阵时，如式(4.4)所示，其结果是行矢量;当将左边的矩阵乘以右边的列矢量时，如式(4.5)所示，其结果是列矢量。
2. 矢量与矩阵乘法的总结：

• 结果矢量中的每个元素是原始矢量与矩阵中的单个行或列的点积。
• 矩阵中的每个元素确定输入矢量中的特定元素对输出矢量中的元素有多大的“权重”。例如，在式(4.4)中，当使用行矢量时，$m_{12}$控制输入的x值有多少输出到了y值。
  矢量与矩阵乘法分布在矢量加法上 (分配律) ，即对于矢量$\pmb{v}、\pmb{w}$和矩阵$\pmb{M}$，有
  
  \pmb
• 乘法的结果是矩阵的行或列的线性组合。例如，在式(4.5)中，当使用列矢量时，得到的列矢量可以被解释为矩阵的列的线性组合，其中的系数来自矢量操作数。这是一个关键事实，不仅对于学习3D数学有用，而且对于一般的线性代数来说也很重要，所以请记住它。

4.1.8 行与列矢量

本节将解释为什么行和列矢量之间的区别很重要，并给出选择行矢量的基本原理。

1. 在式(4.4)中，当将左侧的行矢量与右侧的矩阵相乘时，得到的是以下行矢量:
   

   $$[xm_{11}+ym_{21}+zm_{31} \quad xm_{12}+ym_{22}+zm_{32}\quad xm_{13}+ym_{23}+zm_{33} ]$$

2. 将其与式(4.5)的结果进行比较，当右侧的列矢量乘以左侧的矩阵时，得到的是以下列矢量结果:
   

   $$\left[ \begin{matrix} xm_{11}+ym_{12}+zm_{13} \\ xm_{21}+ym_{22}+zm_{23}\\ xm_{31}+ym_{32}+zm_{33} \end{matrix} \right]$$
   
   如果忽略它们一个是行矢量而另一个是列矢量的事实会发现，矢量分量的值是不一样的!这就是行和列矢量之间的区别如此重要的原因。

3. 行矢量会导致非常“宽”的公式。将列矢量放在右侧肯定会使公式看起来更精简，特别是随着维度的增加，这种差别更加明显。列矢量几乎是所有其他学科中的通用标准

4.2 矩阵的几何解释

1. 一般来说，方形矩阵可以描述任何线性变换(LinearTransformation)线性变换可以“拉伸”坐标空间，但它不会“弯曲”或“扭曲”它。这是一组非常有用的变换，包括:

• 旋转
• 比例缩放
• 正交投影
• 反射
• 错切

2. 第5章将推导出所有执行这些操作的矩阵。先来看以下2x2矩阵:
   

   $$M=\left[ \begin{matrix} 2 & 1 \\ -1 & 2 \end{matrix} \right]$$
   
   这个矩阵代表什么样的变换呢?首先，从矩阵的行中提取基矢量p和q:
   p=[2 1];
   q=[-1 2]
   在图 4.1 中，将+x基矢量变换为上面标记为p的矢量，并将+y基矢量变换为标记为q的矢量。因此，在二维中可视化矩阵的一种方法是可视化由行矢量形成的L形状。在本示例中可以很容易地看到，由矩阵M表示的变换的一部分是大约26.5°的逆时针旋转的。
   
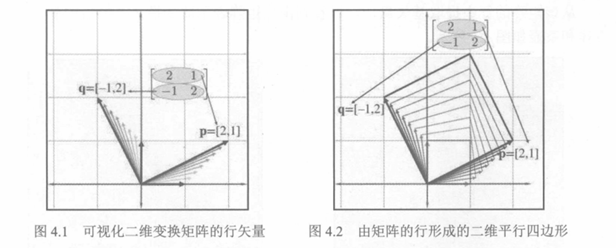
   在图 4.2中形成的这个二维平行四边形也称为倾斜框(Skew Box)。在框内绘制个对象也有助于可视化变换，如图 4.3所示。
   

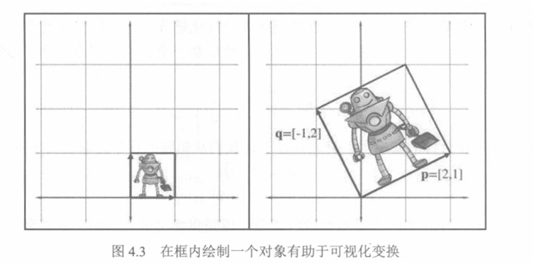
3. 现在考虑三维变换矩阵
   

   $$M=\left[ \begin{matrix} 0.707 & -0.707 & 0 \\ 1.250 & 1.250 & 0 \\ 0 & 0 & 1 \end{matrix} \right]$$
   
   从该矩阵的行中提取基矢量，可以看到由该矩阵表示的变换。变换后的基矢量、立方体和茶壶如图 4.5 所示。
   
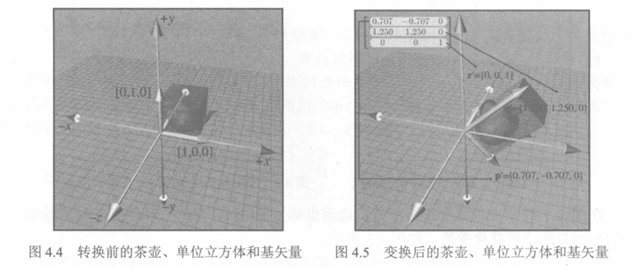
   从图 4.5 中可以看到，变换包括围绕z轴顺时针旋转45°以及使茶壶比原来“更高的非均匀刻度。

4. 本节内容回顾

• 方形矩阵的行可以解释为坐标空间的基矢量。
• 要将矢量从原始坐标空间变换到新坐标空间，可以将失量乘以矩阵。
• 从原始坐标空间到由这些基矢量定义的坐标空间的变换是线性变换。线性变换将保留直线，平行线也将保持平行。但是，角度、长度、面积和体积等可能在变换后发生改变。
• 将零矢量乘以任何方形矩阵，得到的是零矢量。因此，由方形矩阵表示的线性变换将具有与原始坐标空间相同的原点，这意味着变换不包含平移。
• 我们可以通过可视化变换后坐标空间的基失量来可视化矩阵。这些基矢量在二维中会形成L形，而在三维中形成的则是三脚架。使用倾斜框或辅助对象也有助于可视化。

4.3 线性代数的宏大图景

1. 线性代数被发明用于操纵和求解线性方程组。
   
   $$-5x_1+x_2+x_3=-10 \\ 2x_1+2x+2+4x_3=12 \\ x_1-3x_3 = 9$$

的解是

$$x_1=3, \\ x_2=7, \\ x_3=-2$$

2. 上面的方程组和求解结果可以写为以下形式：
   
   $$\left[ \begin{matrix} -5 & 1 & 1 \\ 2 & 2 & 4 \\ 1 & 0 & -3 \end{matrix} \right] \left[ \begin{matrix} x_1\\ x_2\\ x_3 \end{matrix} \right] = \left[ \begin{matrix} -10\\ 12\\ 9 \end{matrix} \right]$$
3. 在游戏中，也许必须求解大型方程组的最直接和最明显的地方是物理引擎。传统线性代数方法出现的另一个常见地方是最小二乘近似(Least Squares Approximation)和其他数据拟合应用。
4. 要学习和理解线性代数和科学计算的宏大图景,推荐一个很好的资源,那就是Gilbert Strang 教授的系列讲座，你可以从ocw.mit.edu的MIT OpenCourseWare(麻省理工学院公
   开课)免费下载。他提供本科阶段基础线性代数课程以及计算科学和工程专业的研究生课程。他为他的班级编写的教科书(详见本书参考文献[67，68])是针对工程师(而不是数学家)的并且让人心情愉快的读物，并且获得了推荐，但要注意他的写作风格是一种速记式的，所以，如果你没有听课，可能会遇到一些理解上的困难。