3D数学基础-图形和游戏开发-学习笔记 第三章 多个坐标空间

开发人员会为特定的理由构建坐标空间（有经验的老手可能会告诉你说“在不同的情况下需要不同的空间”）。

• 3.1 为什么需要多个坐标空间
• 3.2 一些有用的坐标空间
  • 3.2.1 世界空间
  • 3.2.2 对象空间（模型空间）
  • 3.2.3 相机空间（观察空间）
  • 3.2.4 直立空间
• 3.3 基矢量和坐标空间转换
  • 3.3.1 双重视角
  • 3.3.2 指定坐标空间
  • 3.3.3 基矢量
• 3.4 嵌套坐标空间
• 3.5 针对直立空间的再解释

本章主要介绍多个坐标系的概念。它分为以下5个主要小节:- - 第3.1节将证明需要多个坐标系。

• 第3.2节将介绍一些常见的坐标系。介绍的主要概念包括:
  • 世界空间。
  • 对象空间。
  • 相机空间。
  • 垂直空间。
• 第3.3节将描述坐标-空间转换。
  • 第3.3.1节将揭示两种坐标空间转换的思考方式之间的二元性。
  • 第3.3.2节将描述如何根据一个坐标系来指定另一个坐标系。
  • 第3.3.3节将讨论基矢量的非常重要的概念。
• 第3.4节将讨论嵌套坐标空间,它常用于在三维空间中为分层分割对象设置动画。
• 第3.5节将是针对直立空间的强调说明。

3.1 为什么需要多个坐标空间

在不同情况下使用不同的坐标空间会更方便

3.2 一些有用的坐标空间

开发人员需要不同的坐标空间，因为某些信息是有意义的或仅在特定上下文环境中可用。

3.2.1 世界空间

（1）世界坐标系是一个特殊的坐标系，它为所有其他要指定的坐标系建立了一个“全局”参考系。换句话说，我们可以用世界坐标空间来表达其他坐标空间的位置，但是我们不能用任何更大的外部坐标空间来表示世界坐标空间。
（2）世界坐标空间也称为全局(Global）坐标空间或通用(Universal）坐标空间。

3.2.2 对象空间（模型空间）

（1）对象空间（Object Space）是与特定对象关联的坐标空间。
（2）每个对象都有自己独立的对象空间。
（3）当一个对象移动或改变方向时，与该对象关联的对象坐标空间被随之携带，因此它也会移动或改变方向。
（4）可以在对象空间中指定位置和方向。
（5）在图形的上下文中，对象空间也称为模型(Model)空间，因为模型顶点的坐标以模型空间表示。对象空间也称为体（Body)空间，特别是在物理环境中。使用像“相对于体轴”这样的短语也是很常见的，这意味着“使用体空间坐标表示”。

3.2.3 相机空间（观察空间）

（1）对象空间的一个特别重要的示例是相机空间，其是与用于渲染的视点相关联的对象空间。
（2）在相机空间中，相机位于原点，+x指向右侧，+z指向前方（进入屏幕，相机朝向的方向)，+y指向“向上”（注意，这里不是相对于世界的“向上”，而是相对于相机顶部的“向上”）。图3.1显示了相机空间的示意图。

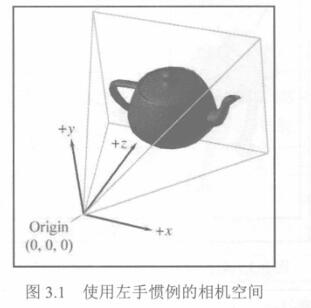
（3）这些是传统的左手坐标系统约定，其他的都很常见。特别要指出的是，OpenGL 传统上是右手坐标系统，-z指向屏幕，+z从屏幕出来朝向观众。
（4）请仔细注意相机空间(三维空间）与屏幕空间（二维空间)之间的差异。从相机空间坐标到屏幕空间坐标的映射涉及的操作称为投影。将在第十章中讨论。

3.2.4 直立空间

（1）当要理解坐标空间转换这个主题时，可以通过文字或通过代码与计算机进行通信，将每个对象与一个新的坐标空间关联在一起，这个新坐标空间我们将其称为对象的直立坐标空间。
（2）在某种意义上，对象的直立空间是世界空间与其对象空间之间的“中间过渡”，因为直立空间的轴线与世界空间的轴线平行，而直立空间的原点则与对象空间的原点重合。下图在二维中说明了这个原理（请注意，我们已经做出了任意选择，将原点放在机器人的脚之间，而不是放在她的质心中）。

（3）在对象空间和直立空间之间转换点只需要旋转；在直立空间和世界空间之间转换点则只需要更改位置，通常称为平移。

（4）下图演示了坐标空间之间的转换。世界空间（图左侧的示意图）可通过平移原点的方式转换为直立空间（图中间的示意图）﹔而为了将直立空间转换为对象空间，可以旋转直立空间的轴直到它们与对象空间的轴对齐。在本示例中，机器人认为她的y轴是从她的脚指向她的头部，并且她的x轴指向她的左边。”我们将在第3.3节中再次讨论这个概念。

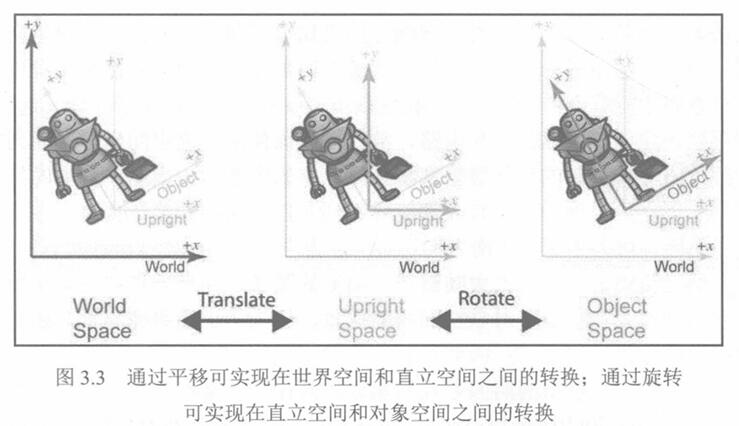
（5）在物理学中，质心坐标一般用来描述直立空间中所表示的坐标。

3.3 基矢量和坐标空间转换

有时某些问题只能在特定的坐标空间中得到解答。

• 3.3.1 将讨论初级视频游戏程序员进场会遇到的转换：图形
• 3.3.2 确保我们清楚根据一个坐标空间指定另一个坐标空间意味着什么。
• 3.3.3 将介绍基矢量(Basis Vector)的主要思想

3.3.1 双重视角

（1）前面的机器人示例，我们只是改变了参考框架并且能够使用不同的坐标空间来描述该点，改变了坐标空间！

如下图所示，将机器人在世界空间的原点进行创建。目前，由于模型处于其原始位置，因此对象空间和世界空间(以及直立空间)根据定义都是相同的。世界空间和对象空间是一致的。

我们的目标是根据在某一时刻可以执行其想法的机器人所期望的位置和方向，将模型的顶点从其原始位置转换到某个新位置(在我们的示例中，就是要进入一间虚构的厨房)，如下图所示

通过旋转和平移的方式最终将机器人从对象空间变换到世界空间。（必须是先旋转，再平移）

（2）围绕原点的旋转是线性变换，而围绕任何其他点的旋转则是仿射变换（在第六章中将对仿射变换进行详细说明）

3.3.2 指定坐标空间

• 指定坐标空间的位置，即描述原点的位置
• 指定坐标空间的方向，即通过告知$+x,+y$的方向来描述.(在二维中还可以通过角度进行方向的描述-极坐标)

3.3.3 基矢量

1. 任意矢量可以扩展为基矢量的线性组合：
   在这里，p、q和r是三维空间的基矢量(Basis Vector)，大多数时候p=[1,0,0],q=[0,1,0],r=[0,0,1]
   
2. 有很多书籍通过用世界基矢量定义所有矢量，“世界基矢量”通常表示为i、j、k，并且被解释为不能进一步分解的元素实体。
3. 当我们说正在使用标准基时，这相当于说，我们只涉及一个单一的坐标空间。这与我们所称的坐标空间没有区别，因为我们无法在不引入基矢量的情况下引用任何其他坐标空间。当我们考虑任何替代基时，则隐式地引入了另一个坐标空间:用于测量基矢量的坐标空间!
4. 基矢量的坐标是根据参考帧测量的，该参考帧与基所在的坐标空间不同。因此，基矢量与坐标空间变换密切相关。
5. 基矢量有可能会选的“很糟糕”，一般会假设他们具有相同的长度且相互垂直(一组相互垂直的基矢量称为正交基，如果长度也相同，那么称为标准正交基)，但有时情况并非如此。
6. 可以表示为基矢量的线性组合的矢量集称为基矢量的跨度。
7. 一组线性相关的矢量对于基来说是一个糟糕的选择。
8. 矢量相对于给定基的数值坐标是该矢量作为基失量的线性组合的扩展中的系数，例
   如，a=$a_x$p+$a_y$q。
9. 当基矢量正交时，坐标是解耦的。矢量v的任何给定坐标可以仅由v和相应的基矢
   量确定。例如，如果其他基矢量垂直于P，那么可以计算仅知道p的$v_x$。
10. 在标准正交基中，矢量v的每个坐标是在对应的基矢量的方向上测量的有符号的位
    移v。这可以通过直接计算v与该基矢量的点积来获得。
    因此，在标准正交基的特殊情况下，有一种简单的方法来确定体空间坐标，只知道
    体轴的世界坐标。因此，假设p、q和r构成标准正交基，
    $b_x$=u·P，
    $b_y$=u·q，
    $b_z$=u·r

3.4 嵌套坐标空间

1. 三维虚拟世界中的每个对象都有自己的坐标空间——它自己的原点和轴。例如，它的原点可以位于其质心处。它的轴将指定它认为相对于其原点的“向上”“向右”“向
   前”的方向。由美术设计师为虚拟世界创建的三维模型将由该设计师决定其原点和轴，并且构成多边形网格的点将相对于由该原点和轴定义的对象空间。例如，绵羊的中心可以
   放置在(0.0.0)，其鼻尖位于(0,0,1.5)，尾部尖端位于(0,0,-1.2)，右耳尖位于(0.5,0.2,1.2)。这些坐标是绵羊的对象空间中这些部分的位置。
   绵羊的各个部分可以利用世界空间的相对位置计算出来。
2. 可以将世界空间视为“父”空间，将对象空间视为“子”空间。还可很方便地将对象分解为子对象并单独为其设置动画。
   分解为这样的层次结构的模型有时被称为关节模型(Articulated Model)。

3.5 针对直立空间的再解释