3D数学基础-图形和游戏开发-学习笔记 第二章 矢量

矢量(Vector)是用于构建2D和3D数学的正式数学单元

目录

• 目录
• 2.1 向量和其他的数学的定义
• 2.2 矢量的几何定义
• 2.3 使用笛卡尔坐标指定矢量
  • 2.3.1 作为位移序列的矢量
  • 2.3.2 零矢量
• 2.4 矢量与点
  • 2.4.1 相对位置
  • 2.4.2 点与矢量之间的关系
• 2.5 负矢量
  • 2.5.1 正式线性代数规则
  • 2.5.2 几何解释
• 2.6 标量和矢量的乘法
  • 2.6.1 正式线性代数规则
  • 2.6.2 几何解释
• 2.7 矢量的加法和减法
  • 2.7.1 正式线性代数规则
  • 2.7.2 几何解释
  • 2.7.3 从一点到另一点的位移矢量
• 2.8 矢量大小
  • 2.8.1 正式线性代数规则
  • 2.8.2 几何解释
• 2.9 单位矢量
  • 2.9.1 正式线性代数规则
  • 2.9.2 几何解释
• 2.10 距离公式
• 2.11 矢量点积
  • 2.11.1 正式线性代数规则
  • 2.11.2 几何解释
• 2.12 矢量叉积
  • 2.12.1 正式线性代数规则
    • 2.12.2 几何解释
  • 2.13 线性代数恒等式

2.1 向量和其他的数学的定义

（1）对于数学家来说，向量是一个数字列表（数组）。数学家会区分向量和标量。标量其实就是普通数字的技术术语。当希望强调特定的数量而不是向量数量时，就会特意使用这个术语。例如，速度（Velocity）和位移（Displacement）都是向量，而速率（Speed）和距离（Distance）则是标量。
向量的维度（Dimension）表示包含的向量的数量。
（2）在书写向量时，会列出由方括号包围的数字，例如[1,2,3]。。当我们用公式写出来时，通常会省略逗号。在任何一种情况下，水平写入的向量称为行向量(Row Vector)。垂直写入的向量称为列向量(Column Vector)。

（3）向量中的各个分量，使用下标表示法，常用x,y,z,w表示一、二、三、四维度中的向量。例如使用x和y来指代二维向量中的元素;使用x、y和z表示三维向量中的元素;使用x、y、z和w表示四维向量中的元素。

（4）书中向量的书写规定。

• 标量变量由斜体字的小写罗马字母或希腊字母表示，如$a、b、x、y、z、\theta、\alpha、\omega和\gamma$等。
• 任何维度的向量变量由粗体小写字母表示，如 a、b、 u、 v、q和r等。
• 矩阵变量使用粗体大写字母表示，如A、B、M和R等。

（5）主要处理向量和矩阵的数学分支称为线性代数（Linear Algebra）

2.2 矢量的几何定义

（1）向量（矢量） 是具有大小和方向的有向线段

• 矢量的大小（Magnitude）是指矢量的长度。矢量可以具有任何非负长度。
• 矢量的方向（Direction）描述矢量在空间中指向的方向。

（2）矢量的示意图

• 示意图能够体现矢量的大小和方向
  

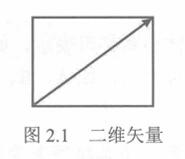
2.3 使用笛卡尔坐标指定矢量

（1）当使用笛卡儿坐标来描述矢量时，每个坐标将度量相应维度中的有符号位移。二维矢量表示示意图如下：

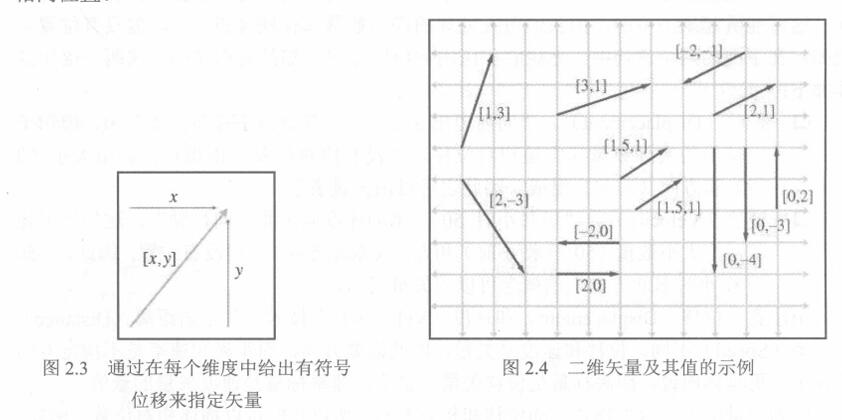
三维矢量是二维矢量的简单扩展。三维矢量包含3个数字，它们可以度量x、y和z方向上的有符号位移。

2.3.1 作为位移序列的矢量

考虑通过矢量描述位移的一种有用方法是将矢量分解为其按轴向对齐的分量。

例如，三维矢量[1,-3,4]表示单个位移，但可以将这个位移可视化如下:①向右移动1个单位;②向下移动3个单位;③向前移动4个单位（这里假设+x、+y和+z分别指向右、向上和向前。

2.3.2 零矢量

（1）零矢量没有方向或长度
（2）任何矢量+零矢量=任何矢量

2.4 矢量与点

点是位置，而矢量指定的是位移

2.4.1 相对位置

（1）因为矢量可以描述位移，所以它们可以描述相对位置。相对位置:某物体的位置通过描述它与其他物体的已知位置之间的关系来指定。

2.4.2 点与矢量之间的关系

如果从原点开始并按矢量[x,y]指定的量移动，那么将最终到达点(x,y)所描述的位置。另一种说法是，矢量[x,y]给出了从原点到点(x,y)的位移。

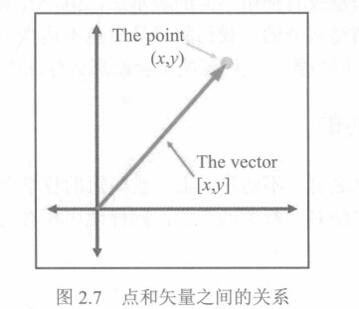
2.5 负矢量

负运算可以应用于矢量。每个矢量$\vec{v}$具有与$\vec{v}$相同维度的加法逆元$-\vec{v}$，使得$\vec{v}+(-\vec{v})=\vec{0}$

2.5.1 正式线性代数规则

为了让任何维度的矢量变负，可以简单地让矢量的每个分量变负

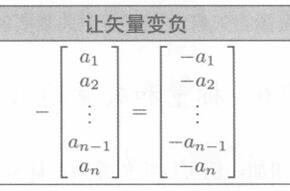
2.5.2 几何解释

使矢量变负会产生大小相同但方向相反的矢量

2.6 标量和矢量的乘法

矢量不可以和标量相加，但可以相乘。结果是一个与原始矢量平行的矢量,但具有不同的长度和可能相反的方向。

2.6.1 正式线性代数规则

表述如下：

大多数人都会选择将标量放在左边

2.6.2 几何解释

在几何上，将矢量乘以标量k具有将长度缩放$|k |$因子的效果。

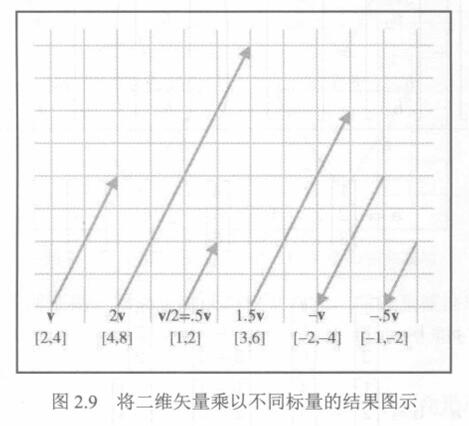
2.7 矢量的加法和减法

如果两个矢量的维度相同，则可以让他们相加。

2.7.1 正式线性代数规则

矢量相加，使用它们相应的分量相加即可。

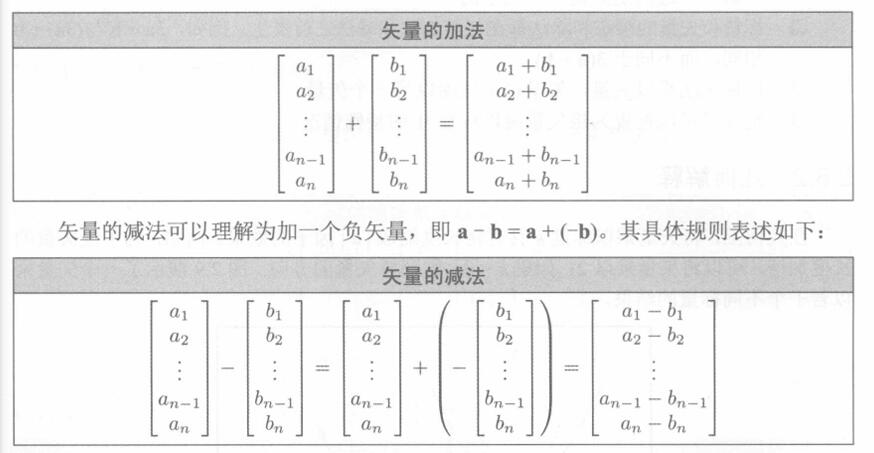
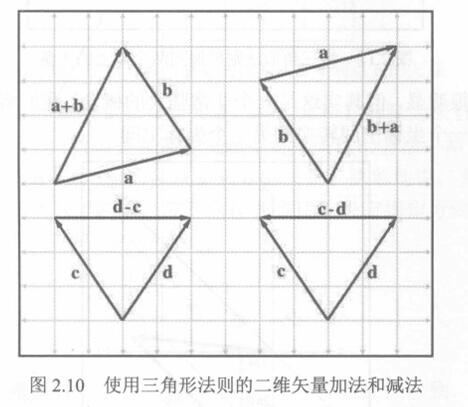
2.7.2 几何解释

向量a与b相加，按几何形式实际上就是使得a的头部接触b的尾部，然后绘制一个从a的尾部到b的头部的矢量。换句话说，如果从一个点开始应用由a指定的位移，然后再应用由b指定的位移，那就像应用了单个位移a+ b一样。这被称为矢量加法的三角形法则。

2.7.3 从一点到另一点的位移矢量

通过矢量加减法即可

2.8 矢量大小

2.8.1 正式线性代数规则

矢量的大小是矢量分量的平方和的平方根。计算方法：

有些图书使用单垂直线符号来表示矢量的大小，即$|v|$。

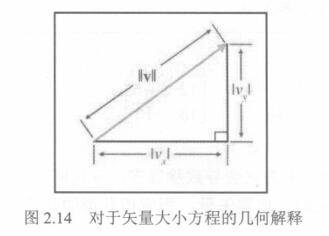
2.8.2 几何解释

对于二维中的任何矢量v，可以形成一个直角三角形,其中v作为斜边，毕达哥拉斯定理指出，对于任何直角三角形，斜边长度的平方等于另外两边长度的平方和。

2.9 单位矢量

单位矢量是大小为1的矢量，单位矢量有时也被称为归一化矢量或者法线。

2.9.1 正式线性代数规则

对于任何非零矢量v，可以计算指向与v相同方向的单位矢量，此过程称为矢量的归一化。为了归一化矢量，可以将矢量除以其大小，具体如下:

2.9.2 几何解释

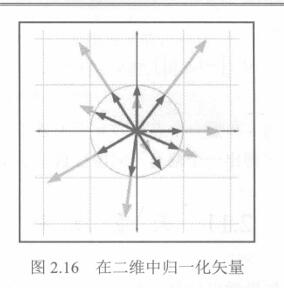
在二维中，如果将单位矢量的尾部绘制在原点处，则矢量的头部将接触到以原点为中心的单位圆(单位圆的半径为1)。在三维中，单位矢量接触到的是单位球面。

2.10 距离公式

距离定义为两点之间的线段长度，先计算两点之间的矢量，然后使用2.8中提到的矢量大小求法，求矢量的长度，即为两点之间的距离。

2.11 矢量点积

点积在较多地方都有使用，例如矩阵乘法、信号卷积、统计相关和傅立叶变换等。

2.11.1 正式线性代数规则

“点积”的名称来自矢量乘积表示法中使用的点符号:$a·b$。两个矢量的点积是相应分量的乘积之和,得到的是一个标量。

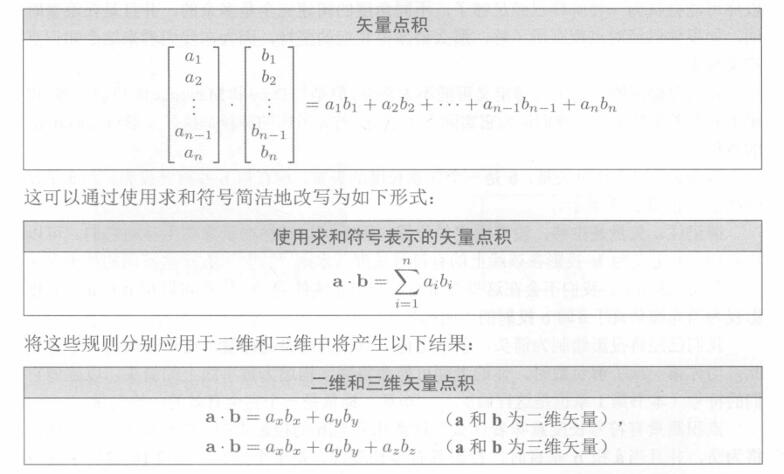
2.11.2 几何解释

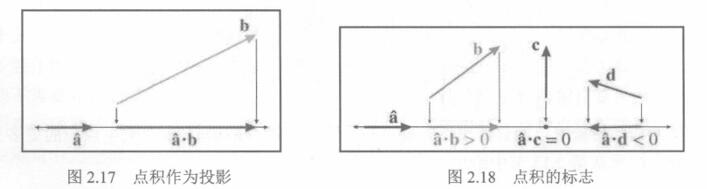
1. 两个非零矢量$\vec{a},\vec{b}$点积运算，实际上就是一个矢量在另一个矢量上的投影长度。

• 当$\vec{a}$与$\vec{b}$方向相同，结果为正
• 当$\vec{a}$与$\vec{b}$方向相反，结果为负
  

2. 点积结合律
   

3. 点积交换律
   当两个矢量a和b都是单位矢量时，可以很容易地得出一个几何论证，即a在b上的投影与b在a上的投影具有相同的长度。考虑下图，两个三角形具有相等的内角，因此它们是相似的。由于a和b是对应的边并且具有相同的长度，因此两个三角形是彼此的反射。
   

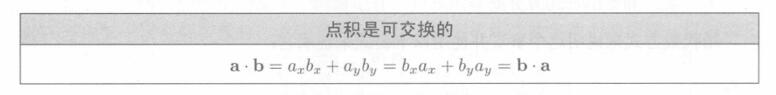
4. 点积分配律
   
   

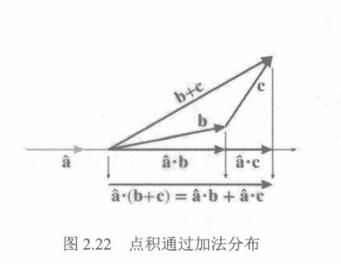
5. 自身的点积
   矢量投影到自身上，则该投影的长度就是矢量的大小。但要记住，a·b等于b投影到a上的长度，并且按||a||缩放。如果用矢量自身计算矢量点积，例如v·v，则得到的是投影的长度（即|||v||）乘以投射到的矢量的长度。
   

6. 点积与截取角度的关系
   (1) 根据点积求截取角度
   
   
   (2) 根据点积结果，得到向量的方向关系
   

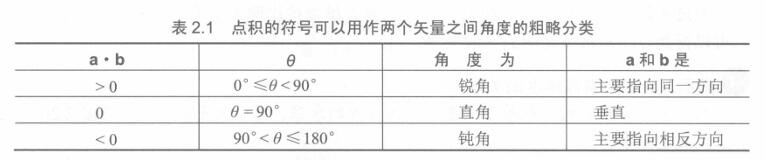
7. 总结

• 点积a·b将测量b投影到a上的长度，乘以a的长度。
• 点积可用于测量特定方向的位移。
  投影运算与余弦函数密切相关。点积a·b也等于||a||||b||$cos\theta$，其中，$\theta$是矢量之间的角度。

2.12 矢量叉积

2.12.1 正式线性代数规则

1. 叉积的表示为 axb ,其中的“×”不能像标量一样省略。
2. 叉积的公式：

$$\left[\begin{aligned}\ x_1\\ y_1\\ z_1\\ \end{aligned}\right] \times \left[\begin{aligned}\ x_2\\ y_2\\ z_2\\ \end{aligned}\right]= \left[\begin{aligned}\ y_1z_2-z_1y_2\\ z_1x_2-x_1z_2\\ x_1y_2-y_1x_2\\ \end{aligned}\right]$$

1. 叉积和点积具有相同的运算符优先级：乘法正在加减法之前。当点积和叉积一起使用时，叉积优先：
   $$\vec{a}·\vec{b}\times\vec{c}=\vec{a}·(\vec{b}\times\vec{c})$$
   ，因为如果先算了点积的话，不能采用标量和矢量的叉积。
2. 叉积的反交换：
   $$\vec{a}\times\vec{b}=-(\vec{b}\times\vec{a})$$

2.12.2 几何解释

1. 叉积将产生一个矢量，垂直于原始的两个矢量。a×b的长度等于a和b的大小的乘积再乘以a和b之间角度的正弦值。
   
   

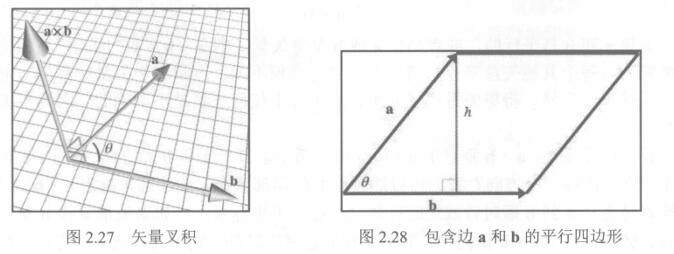
2. 基本轴的叉积
   可以使用1.3.3节中使用手的方法来求叉积的基本轴
   

2.13 线性代数恒等式